(遂宁)如图,▱ABCD中,点E,F在对角线BD上,且BE=DF,求证: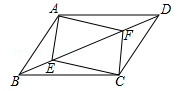
(1)AE=CF;
(2)四边形AECF是平行四边形.
已知直线y=-x+6和反比例函数y= (k≠0)
(k≠0)
(1)k满足什么条件时,这两个函数在同一坐标系xOy中的图象有两个公共点?
(2)设(1)的两个公共点分别为A、B,∠AOB是锐角还是钝角?
某厂要制造能装250mL(1mL=1cm3)饮料的铝制圆柱形易拉罐,易拉罐的侧壁厚度和底部厚度都是0.02cm,顶部厚度是底部厚度的3倍,这是为了防止“砰”的一声打开易拉罐时把整个顶盖撕下来,设一个底面半径是x cm的易拉罐用铝量是y cm3.用铝量=底面积×底部厚度+顶部面积×顶部厚度+侧面积×侧壁厚度,求y与x间的函数关系式.
已知一个三角形的面积是12cm2
(1)写出一边y(cm)与该边上的高x(cm)间的函数关系式;
(2)画出函数图象.
若反比例函数y=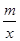 与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时,这两个函数值相等,求反比例函数解析式.
与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时,这两个函数值相等,求反比例函数解析式.
如图,Rt△AOB的顶点A是一次函数y=-x+m+3的图象与反比例函数y=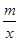 的图象在第二象限的交点,且S△AOB=1,求点A的坐标.
的图象在第二象限的交点,且S△AOB=1,求点A的坐标.