如图,已知反比例函数y= 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.
(1)计算:2cos45°-(π+1)0+ +
+
(2)解方程:x(2x-5)=4x-10.
我校需刻录一批电脑光盘,若到电脑公司刻录,每张需要4元(包括空白光盘费);若学校自刻,除买刻录机60元外,每张还需成本2元(包括空白光盘费),问刻录这批电脑光盘,到电脑公司刻录费用省,还是自刻费用省?请说明理由.
小明手中有3000元压岁钱,爸妈要他学习投资理财.小明想买年利率为2.89%的三年期国库卷,到银行时,银行所剩国库卷已不足3000元,小明全部买下着国库卷后,余下的钱改成三年定期银行存款,年利率为2.7%,且到期要交纳20%的利息税,三年后,小明得到的本息和为3233.82元,小明到底买了多少的国库卷,在银行存款又是多少元?
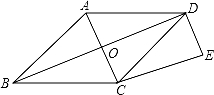
如图,O是菱形ABCD对角线的交点,作DE∥AC,CE∥BD,DE、CE交于点E,四边形OCED是矩形吗?说说你的理由.