已知函数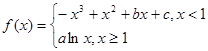 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点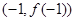 处的切线的斜率是
处的切线的斜率是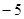 .
.
(Ⅰ)求实数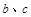 的值;
的值;
(Ⅱ)求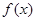 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线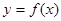 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得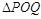 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由.
轴上?说明理由.
在 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,已知
,已知 .
.
(1)求 及
及 的面积
的面积 ;
;
(2)求 .
.
已知四棱锥P-ABCD,底面ABCD是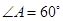 的菱形,又
的菱形,又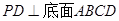 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.
(Ⅰ)证明:DN//平面PMB;
(Ⅱ)证明:平面PMB 平面PAD;
平面PAD;
解关于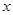 的不等式
的不等式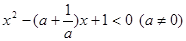
已知函数f(x)的定义域为(-2,2),函数g(x)=f(x-1)+f(3-2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
函数f(x)是R上的奇函数,且当x>0时,函数的解析式为 .
.
(1)用定义证明f(x)在(0,+∞)上是减函数;
(2)求当x<0时,函数的解析式.
(3)用分段函数形式写出函数f(x)在R上的解析式.当f(a)=3时,求a的值。