已知椭圆C: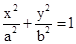 (a>b>0)的离心率为
(a>b>0)的离心率为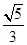 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3.
(1)求椭圆C的方程;
(2)过椭圆C上的动点P引圆O:x2+y2=b2的两条切线PA、PB,A、B分别为切点,试探究椭圆C上是否存在点P,由点P向圆O所引的两条切线互相垂直?若存在,请求出点P的坐标;若不存在,请说明理由.
设函数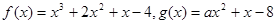
(1)求函数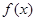 极值;
极值;
(2)当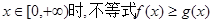 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
(本题满分14分)
如图所示,在正三棱柱ABC -A1B1C1中,底面边长和侧棱长都是2,D是侧棱CC1上任意一点,E是A1B1的中点。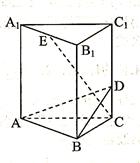
(I)求证:A1B1//平面ABD;
(II)求证:AB⊥CE;
(III)求三棱锥C-ABE的体积。
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
在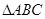 中,已知
中,已知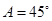 ,
,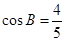 .
.
(Ⅰ)求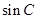 的值;
的值;
(Ⅱ)若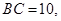 求
求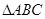 的面积.
的面积.