(本小题满分12分)
已知点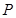 为圆
为圆 上的动点,且
上的动点,且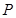 不在
不在 轴上,
轴上,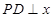 轴,垂足为
轴,垂足为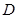 ,线段
,线段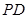 中点
中点 的轨迹为曲线
的轨迹为曲线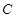 ,过定点
,过定点
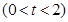 任作一条与
任作一条与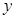 轴不垂直的直线
轴不垂直的直线 ,它与曲线
,它与曲线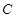 交于
交于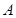 、
、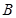 两点。
两点。
(I)求曲线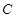 的方程;
的方程;
(II)试证明:在 轴上存在定点
轴上存在定点 ,使得
,使得 总能被
总能被 轴平分
轴平分
(1) 已知集合 ,若
,若 ,求实数
,求实数 的值
的值
(2)已知集合A={x|x2-5x-6=0},集合B={x|mx+1=0}若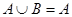 ,求实数m组成的集合.
,求实数m组成的集合.
已知函数f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1
(1)求f(1)的值
(2)若满足f(x) +f(x-8)≤2 求x的取值范围
设函数 ,其中
,其中
(I)当 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性;
(II)求函数 的极值点;
的极值点;
(III)证明对任意的正整数n ,不等式 都成立.
都成立.
设a∈R,函数f(x)=lnx-ax.
(1)讨论函数f(x)的单调区间和极值;
(2)已知 (e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e
(e为自然对数的底数)和x2是函数f(x)的两个不同的零点,求a的值并证明:x2>e .
.
已知函数 (
( R,
R, ,
, ,
, )图象如图,P是图象的最高点,Q为图象与
)图象如图,P是图象的最高点,Q为图象与 轴的交点,O为原点.且
轴的交点,O为原点.且 ,
, ,
, .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)将函数 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数 的图象,当
的图象,当 时,求函数
时,求函数 的最大值.
的最大值.