如图，已知梯形ABCD的下底边长AB＝8cm，上底边长DC＝1cm，O为AB的中点，梯形的高DO＝4cm. 动点P自A点出发，在AB上匀速运行，动点Q自点B出发，沿B→C→D→A匀速运行，速度均为每秒1个单位，当其中一个动点到达终点时，另一动点也同时停止运动. 设点P运动t（秒）时，△OPQ的面积为S（不能构成△OPQ的动点除外）.
（1）求S随t变化的函数关系式及t的取值范围；
（2）当t为何值时S的值最大？说明理由.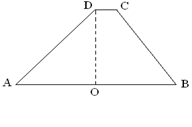
（本小题满分10分）
如图l所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线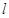
∥BC，交直线CD于点F．将直线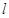向右平移，设平移距离BE为
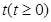，直角梯形ABCD被直线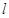扫过的面积（图中阴影部分）为S，S关于
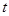的函数图象如图2所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．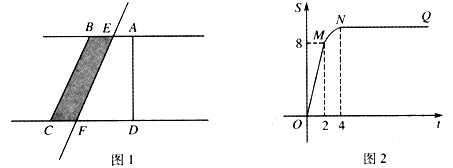
（1）AB=________；CD=__________；梯形ABCD的面积为_______（直接写出答案）；
（2）当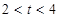
时，求S关于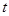的函数关系式；
（3）当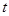为何值时，直线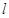将直角梯形ABCD分成的两部分面积之比为1：3．
（本小题满分8分）
使得函数值为零的自变量的值称为函数的零点．例如，对于函数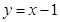
，令
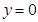，可得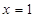
，我们就说1是函数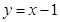的零点．
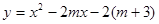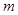已知函数
（
为常数）．
（1）当
时，求该函数的零点；
（2）证明：无论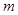取何值，该函数总有两个零点．
（本小题满分8分）
如图，在△ABC中，D是AC的中点，E是线段BC延长线上一点，过点A作BE的平行线AF与线段ED的延长线交予点F，连接AE，EF．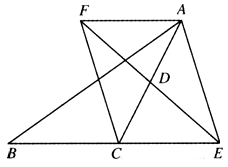
（1）求证：AF=CE；
（2）如果AC=EF，且∠ACB=135°,试判断四边形AFCE是什么样的四边形，并证明你的结论．
（本小题满分8分）
某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．
（1）求该校八年级学生参加社会实践活动的人数；
（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1 500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．
请你计算本次社会实践活动所需车辆的租金．
（本小题满分8分）
已知一次函数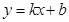
的图象与直线
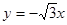平行且经过点（2，
），与
轴、
轴分别交于A，B两点．
（1）求此一次函数的解析式；
（2）过坐标原点O作OC⊥AB交AB于点C，求OC的长．