已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).
(1)求二次函数的解析式;
(2)填空:要使该二次函数的图象与x轴只有一个交点,
应把图象沿y轴向上平移 __________ 个单位.
(本题6分)
(1)制作一个表面积为12平方分米的正方体纸盒,棱长应为多少分米?
(2)如果2a-1的平方根是±3,3a+2b+4的立方根是3,求a+b的平方根.
化简计算:(本题满分题6分)
(1)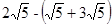 (2)
(2)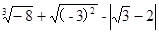
如图1,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.
(1)试猜想线段BG和AE的数量关系是;
(2)将正方形DEFG绕点D逆时针方向旋转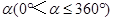 ,
,
①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
②若BC=DE=4,当AE取最大值时,求AF的值.(可另外画图)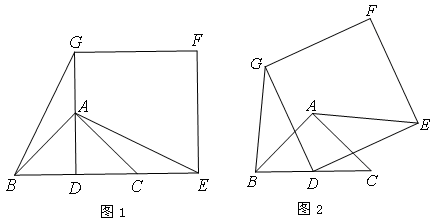
已知:四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.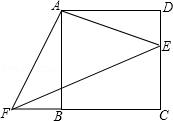
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心点,按顺时针方向旋转度得到;
(3)若BC=8,DE=6,求△AEF的面积.
已知在矩形ABCD中,E为DC边上一点BF⊥AE于点F,且BF=BC。求证:AE=AB。