（本题6分）
（1）制作一个表面积为12平方分米的正方体纸盒，棱长应为多少分米？
（2）如果2a－1的平方根是±3，3a+2b+4的立方根是3，求a+b的平方根．
（本小题满分10分）
如图，AB是⊙O的直径，弦DE垂直平分半径OA，垂足为C，弦DF与半径OB相交于点P．连结EF，EO ．若DE=
，∠DPA=45°
（1）求⊙O的半径；
（2）求图中阴影部分的面积．（结果保留两个有效数字）
（本小题满分10分）
设函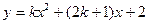数
（
为任意实数）（1）求证：不论
为何值，该函数图象都过点（0，2）和（－2，0）；（2）若该函数图象与
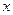轴只有一个交点，求的值．
（本小题满分8分）
已知：如图，在⊙O中，AB=CD．
求证：∠ABD=∠CDB
（本小题满分8分）
如图，一次函数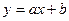
的图象与反比例函数
的图象交于
、
两点．（1）利用图中条件，求反比例函数和一次函数的解析式；
（2）根据图象直接写出使反比例函数的值
大于一次函数的值的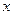
的取值范围．
（本小题满分6分）
已知抛物线的解析式为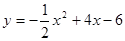
（1）求抛物线的顶点坐标；
（2）求出抛物线与x轴的交点坐标；
（3）当x取何值时y>0？