联合国规定每年的月日是“世界环境日”,为配合今年的“世界环境日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环境,从我做起”为主题的问卷调查活动,将调查结果分析整理后制成了下面的两个统计图.其中:
| A．能将垃圾放到规定的地方，而且还会对垃圾分类。 | B．能将垃圾放到规定地方，但不会考虑垃圾分类。 | C．偶尔会将垃圾放到规定的地方。 | D．随手乱扔垃圾。 根据以上信息回答下列问题： |
(1)该校课外活动小组共调查了多少人?并补全上面的条形统计图;
(2)如果该校共有师生2400人,那么随手乱扔垃圾的约有多少人?
（本小题满分8分）如图，“五·一”期间在某商贸大厦上从点A到点B悬挂了一条宣传条幅，小明和小雯的家正好住在商贸大厦对面的家属楼上，小明在四楼D点测得条幅端点A的仰角为30°，测得条幅端点B的俯角为45°；小雯在三楼C点测得条幅端点A的仰角为45°，测得条幅端点B的俯角为30°．若设楼层高度CD为3米，请你根据小明和小雯测得的数据求出条幅AB的长．（结果精确到个位，参考数据
≈1．73）
（本小题满分6分）如图，4张背面完全相同的纸牌（用①、②、③、④表示），在纸牌的正面分别写有四个个不同的条件，小明将这4张纸牌背面朝上洗匀后，先随机摸出一张（不放回），再随机摸出一张．
（1）用列表法（或树状图法）表示两次摸牌出现的所有可能结果（用①、②、③、④表示）；
（2）以两次摸出牌上的结果为条件，求能判断四边形ABCD是平行四边形的概率．
（本小题满分5分）如图，四边形ABCD为正方形，利用尺规作图在正方形ABCD内（含边），画出使∠APB=60°的所有的点构成的图形．（要求：不写作法，保留作图痕迹，写出结论）
（本小题满分10分，每小题5分）
（1）计算：
；
（2）解方程：
+3x－1=0．
已知：如图，点A（3，4）在直线y=kx上，过A作AB⊥x轴于点B．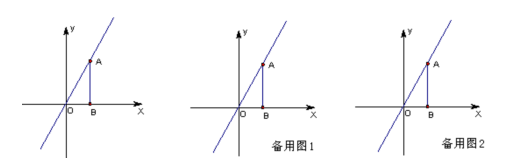
（1）求k的值；
（2）设点B关于直线y=kx的对称点为C点，求ΔABC外接圆的面积；
（3）抛物线y=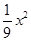
－1与x轴的交点为Q，试问在直线y=kx上是否存在点P，使得∠CPQ=∠OAB，如果存在，请求出P点的坐标；如果不存在，请说明理由．