如图1，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．
（1）求证：△DEC≌△EDA；
（2）求DF的值；
（3）如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其定点Q落在线段AE上，定点M、N落在线段AC上，求当线段PE的长为何值时，矩形PQMN的面积最大？
如图，一次函数的图象与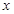
轴、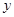
轴分别相交于A、B两点，且与反比例函数的图象在第二象限交于点C．如果点A的坐标为
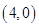，OA=2OB，点 B是AC的中点．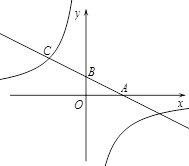
（1）求点C的坐标；
（2）求一次函数和反比例函数的解析式．
如图，BC为⊙O的直径，以BC为直角边作Rt△ABC，∠ACB=90°，斜边AB与⊙O交于点D，过点D作⊙O的切线DE交AC于点E，DG⊥BC于点F，交⊙O于点G．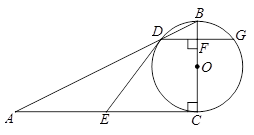
（1）求证：AE=CE；
（2）若AD=4，AE=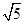
，求DG的长．
如图，点P是菱形ABCD的对角线BD上一点，连结AP、CP，延长CP交AD于E，交BA的延长线于F．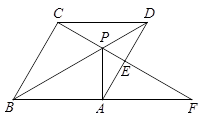
（1）求证：∠DCP=∠DAP；
（2）若AB=2，DP:PB=1:2，且PA⊥BF，求对角线BD的长．
如图，抛物线经过点A、B、C．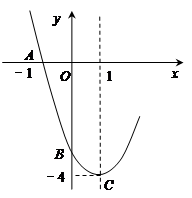
（1）求此抛物线的解析式；
（2）若抛物线和x轴的另一个交点为D，求△ODC的面积．
如图，已知AB为⊙O的直径，CD是弦，且AB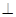
CD于点E．连接AC、OC、BC．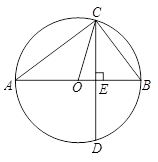
（1）求证：∠ACO=∠BCD．
（2）若BE=3，CD=8，求⊙O的直径．