如图,一次函数的图象与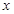 轴、
轴、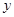 轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为
轴分别相交于A、B两点,且与反比例函数的图象在第二象限交于点C.如果点A的坐标为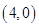 ,OA=2OB,点 B是AC的中点.
,OA=2OB,点 B是AC的中点.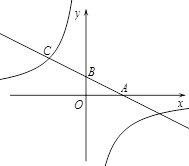
(1)求点C的坐标;
(2)求一次函数和反比例函数的解析式.
已知:如图所示,四边形ABCD是矩形,对角线AC,BD相交于点O,CE//DB,交AB的延长线于点E,AC与CE相等吗?请说明理由。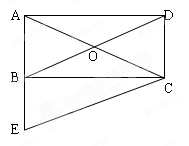
如图,四边形ABCD中,AB∥CD,AC平分∠BAD ,CE∥AD交AB于点E。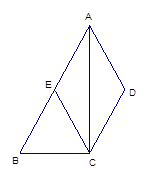
(1)判断:四边形AECD是什么形状?并给出理由。
(2)若点E是AB的中点,是判断△ABC的形状,并给出理由。
做图:在△ABC中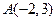 ,
,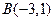 ,
,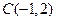 .
.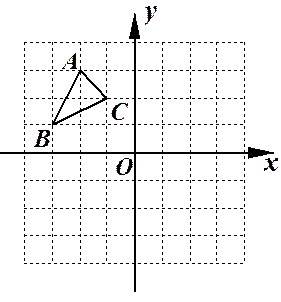
(1)将△
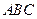 向右平移4个单位长度,画出平移后的△
向右平移4个单位长度,画出平移后的△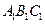 ;
;(2)画出△
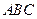 关于
关于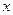 轴对称的△
轴对称的△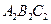 ;
;(3)将△
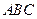 绕原点O旋转180º,画出旋转后的△
绕原点O旋转180º,画出旋转后的△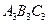 ;
;(4)在△
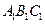 .△
.△
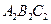 .△
.△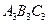 中,
中,
△ 与 △ 成轴对称,对称轴是 ;
△ 成轴对称,对称轴是 ;
△ 与△ 成中心对称,对称中心的坐标是
(8分)一根祝寿蜡烛长85cm,点燃时每小时缩短5cm。(1)请写出点燃后蜡烛的长y(cm)与蜡烛燃烧时间t(h)之间的函关系式;
(2)该蜡烛可点燃多长时间?
(本小题满分12分)
如图(1),△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△EFD绕点A 顺时针旋转,当DF边与AB边重合时,旋转中止。不考虑旋转开始和结束时重合的情况,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H点,如图(2)。
(1)问:始终与△AGC相似的三角形有及;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据2的情况说明理由);
(3)问:当x为何值时,△AGH是等腰三角形?