做图:在△ABC中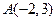 ,
,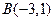 ,
,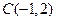 .
.
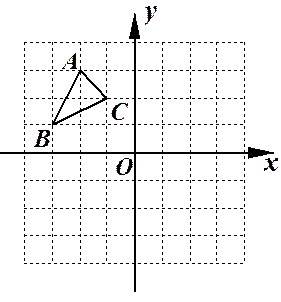
(1)将△
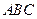 向右平移4个单位长度,画出平移后的△
向右平移4个单位长度,画出平移后的△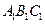 ;
;
(2)画出△
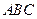 关于
关于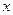 轴对称的△
轴对称的△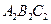 ;
;
(3)将△
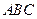 绕原点O旋转180º,画出旋转后的△
绕原点O旋转180º,画出旋转后的△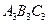 ;
;
(4)在△
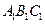 .△
.△
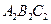 .△
.△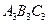 中,
中,
△ 与 △ 成轴对称,对称轴是 ;
△ 成轴对称,对称轴是 ;
△ 与△ 成中心对称,对称中心的坐标是
列方程解应用题:某学校在援助边远山区学校活动中,原计划赠书3000册,由于学生的积极响应,实际赠书3780册,其中初中部比原计划多赠了20%,高中部比原计划多赠了30%,该校初、高中部原计划各赠书多少册?
列方程解应用题:出租车10元起价,行驶4km以后,每增加1km加价1.2元(不足1km部分按1km计).小明要乘出租车去10km外的叔叔家,出门时只拿了16元钱,小明能否乘出租车直接到叔叔家?(不计等候时间)
列方程解应用题:甲、乙两班计划共同植树360棵,结果由于同学们的积极努力,甲班超额完成计划的12%,乙班超额完成计划的10%,因此,两班实际植树400棵.甲、乙两班原计划各植多少棵树?
列方程解应用题:一群学生前往位于青田县境内的滩坑电站建设工地进行社会实践活动,男生戴白色安全帽,女生戴红色安全帽,休息时他们坐在一起,大家发现了一个有趣的现象,每名男生看到白色与红色的安全帽一样多,而每名女生看到白色安全帽是红色的2倍.
根据这些信息,请你推测这群学生共有多少人?
列方程解应用题:要加工210个零件,甲、乙两人一起加工6小时后,甲生病离开,余下的任务由乙单独加工,乙又用了4小时完成,如果甲每小时比乙多加工3个零件,那么甲、乙两人每小时各加工多少零件?