如图,已知AB为⊙O的直径,CD是弦,且AB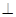 CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.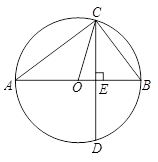
(1)求证:∠ACO=∠BCD.
(2)若BE=3,CD=8,求⊙O的直径.
计算:
解方程: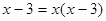
如图,直线y=-x+20与x轴、y轴分别交于A、B两点,动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动. 动直线EF从x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴),并且分别与y轴、线段AB交于E、F点. 连结FP,设动点P与动直线EF同时出发,运动时间为t秒.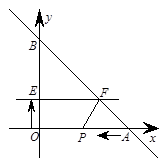
(1) 当t=1秒时,求梯形OPFE的面积;
(2) t为何值时,梯形OPFE的面积最大,最大面积是多少?
(3) 设t的值分别取t1、t2时(t1≠t2),所对应的三角形分别为△AF1P1和△AF2P2.试判断这两个三角形是否相似,请证明你的判断.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC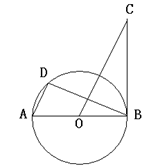
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=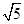 ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为: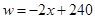 ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为y(元),解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果公司想要在这段时间内获得2250元的销售利润,销售单价应定为多少元?