如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC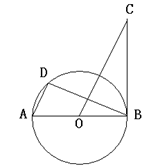
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=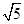 ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
如图,已知二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,直线 经过 , 两点.
(1)直接写出二次函数的解析式 ;
(2)平移直线 ,当直线 与抛物线有唯一公共点 时,求此时点 的坐标;
(3)过(2)中的点 作 轴,交 轴于点 .若点 是抛物线上一个动点,点 是 轴上一个动点,是否存在以 , , 三点为顶点的直角三角形(其中 为直角顶点)与 相似?如果存在,请直接写出满足条件的点 的个数和其中一个符合条件的点 的坐标;如果不存在,请说明理由.

阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
如图, 是 的直径, 是 的一条弦,点 是 上一点,且 , ,与 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求直径 的长.

甲、乙两支工程队修建二级公路,已知甲队每天修路的长度是乙队的2倍,如果两队各自修建公路 ,甲队比乙队少用5天.
(1)求甲,乙两支工程队每天各修路多少米?
(2)我市计划修建长度为 的二级公路,因工程需要,须由甲、乙两支工程队来完成.若甲队每天所需费用为1.2万元,乙队每天所需费用为0.5万元,求在总费用不超过40万元的情况下,至少安排乙队施工多少天?
如图1,一枚质地均匀的正四面体骰子,它有四个面,并分别标有1,2,3,4四个数字;如图2,等边三角形 的三个顶点处各有一个圆圈.丫丫和甲甲想玩跳圈游戏,游戏的规则为:游戏者从圈 起跳,每投掷一次骰子,骰子着地的一面点数是几,就沿着三角形的边逆时针方向连续跳跃几个边长.如:若第一次掷得点数为2,就逆时针连续跳2个边长,落到圈 ;若第二次掷得点数为4,就从圈 继续逆时针连续跳4个边长,落到圈 .
(1)丫丫随机掷一次骰子,她跳跃后落回到圈 的概率为 ;
(2)丫丫和甲甲一起玩跳圈游戏:丫丫随机投掷一次骰子,甲甲随机投掷两次骰子,都以最终落回到圈 为胜者.这个游戏规则公平吗?请说明理由.
