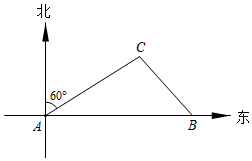
如图,已知二次函数 的图象与 轴交于 , 两点,与 轴交于点 ,直线 经过 , 两点.
(1)直接写出二次函数的解析式 ;
(2)平移直线 ,当直线 与抛物线有唯一公共点 时,求此时点 的坐标;
(3)过(2)中的点 作 轴,交 轴于点 .若点 是抛物线上一个动点,点 是 轴上一个动点,是否存在以 , , 三点为顶点的直角三角形(其中 为直角顶点)与 相似?如果存在,请直接写出满足条件的点 的个数和其中一个符合条件的点 的坐标;如果不存在,请说明理由.

如图,在平面直角坐标系中,已知点 的坐标为 ,且 ,抛物线 图象经过 , , 三点.
(1)求 , 两点的坐标;
(2)求抛物线的解析式;
(3)若点 是直线 下方的抛物线上的一个动点,作 于点 ,当 的值最大时,求此时点 的坐标及 的最大值.
如图, 是 的直径,弦 与 相交于点 , 与 相切于点 ,交 的延长线于点 , , , .
(1)求 的度数;
(2)求 的长度.

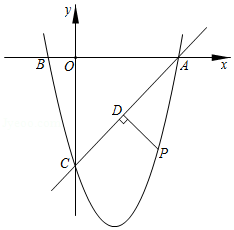
如图,在矩形 中, , 分别是 , 边上的点,且 .
(1)求证: ;
(2)当 时,四边形 是菱形吗?请说明理由.
2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
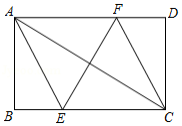
如图,在 处的正东方向有一港口 .某巡逻艇从 处沿着北偏东 方向巡逻,到达 处时接到命令,立刻在 处沿东南方向以20海里 小时的速度行驶3小时到达港口 .求 , 间的距离. , , ,结果保留一位小数).