在平面直角坐标系中,抛物线y=ax2+bx+2的图象过 和
和 ,与
,与 轴交于点
轴交于点 ,与
,与 轴交于另一点
轴交于另一点 ,点
,点 是原点
是原点 关于点
关于点 的对称点,连结
的对称点,连结 、
、 ,设点
,设点 。
。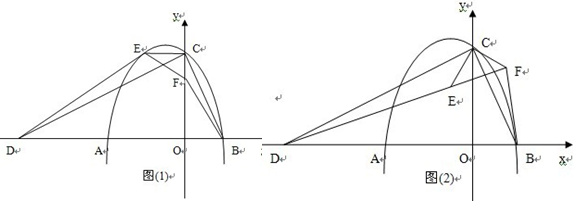
(1)求抛物线的解析式;
(2)连结 、
、 ,①求
,①求 的值;②将
的值;②将 绕点
绕点 旋转,在旋转过程中如图(2),线段
旋转,在旋转过程中如图(2),线段 和
和 的比值会变吗?请说明理由;
的比值会变吗?请说明理由;
(3)设点 是直线
是直线 上方的抛物线上一点,连结
上方的抛物线上一点,连结 ,以
,以 为边作图示一侧的正方形,随着点
为边作图示一侧的正方形,随着点 的运动,正方形的大小,位置也随之改变,当顶点
的运动,正方形的大小,位置也随之改变,当顶点 或
或 恰好落在
恰好落在 轴上时,直接写出对应点
轴上时,直接写出对应点 的坐标。
的坐标。
解不等式组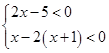 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
计算:
使得函数值为零的自变量的值称为函数的零点.例如,对于函数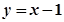 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数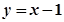 的零点.请根据零点的定义解决下列问题:已知函数
的零点.请根据零点的定义解决下列问题:已知函数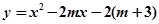 (m为常数).
(m为常数).当m=0时,求该函数的零点
证明:无论m取何值,该函数总有两个零点;
设函数的两个零点分别为
 和
和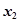 ,且
,且 ,此时函数图象与
,此时函数图象与 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线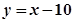 上,当MA+MB最小时,求直线AM的函数解析式.
上,当MA+MB最小时,求直线AM的函数解析式.
如图(1),AB、BC、CD分别与⊙O相切于点E、F、G,且AB∥CD,若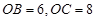 ,
,
求BC和OF的长;
求证:
 三点共线;
三点共线;小叶从第(1)小题的计算中发现:等式
 成立,于是她得到这样的结论:如图(2),在
成立,于是她得到这样的结论:如图(2),在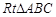 中,
中,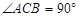 ,
,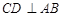 ,垂足为
,垂足为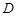 ,设
,设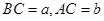 ,
, ,则有等式
,则有等式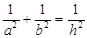 成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.
成立.请你判断小叶的结论是否正确,若正确,请给予证明,若不正确,请说明理由.
如图,直线l经过点A(1,0),且与曲线 (x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线
(x>0)交于点B(2,1).过点P(p,p-1)(p≥2)作x轴的平行线分别交曲线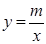 (x>0)和
(x>0)和 (x<0)于M,N两点.
(x<0)于M,N两点.
求m的值及直线l的解析式;
是否存在实数p,使得S△AMN=4S△APM?若存在,请求出所有满足条件的p的值;若不存在,请说明理由