小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图: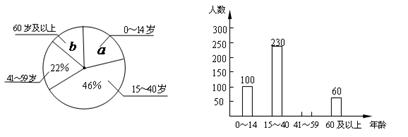
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中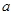 = ;
= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4) 若该辖区年龄在0~14岁的居民约有3500人,请估计该辖区居民人数是
人.
善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量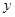 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间 (单位:分钟)与学习收益
(单位:分钟)与学习收益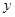 的关系如图2所示(其中
的关系如图2所示(其中 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量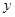 与用于解题的时间
与用于解题的时间 之间的函数关系式;
之间的函数关系式;
(2)求小迪回顾反思的学习收益量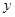 与用于回顾反思的时间
与用于回顾反思的时间 的函数关系式;
的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?




如图,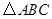 内接于
内接于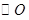 ,点
,点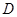 在半径
在半径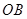 的延长线上,
的延长线上,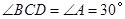 .
.
(1)试判断直线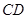 与
与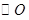 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若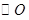 的半径长为1,求由弧
的半径长为1,求由弧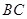 、线段
、线段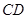 和
和 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留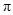 和根号).
和根号).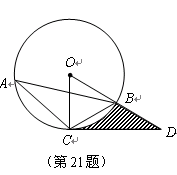
把正方形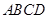 绕着点
绕着点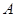 ,按顺时针方向旋转得到正方形
,按顺时针方向旋转得到正方形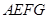 ,边
,边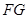 与
与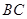 交于点
交于点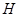 (如图).试问线段
(如图).试问线段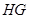 与线段
与线段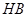 相等吗?请先观察猜想,然后再证明你的猜想.
相等吗?请先观察猜想,然后再证明你的猜想.
先化简,再求值: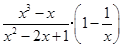 ,其中
,其中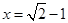 .
.