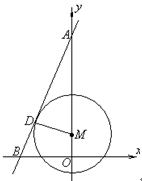
如图, 已知直线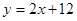 分别与
分别与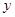 轴,
轴, 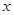 轴交于
轴交于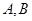 两点, 点
两点, 点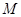 在
在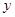 轴上. 以点
轴上. 以点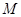 为圆心的⊙
为圆心的⊙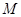 与直线
与直线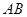 相切于点
相切于点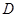 , 连接
, 连接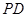 .
.
(1) 求证:  ∽
∽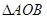 ;
;
(2)如果⊙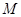 的半径为
的半径为 , 求出点
, 求出点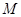 的坐标, 并写出以
的坐标, 并写出以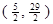 为顶点, 且过点
为顶点, 且过点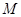 的抛物线的解析式;
的抛物线的解析式;
(3) 在(2)的条件下, 在此抛物线上是否存在点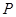 , 使得以
, 使得以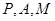 三点为顶点的三角形与
三点为顶点的三角形与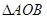 相似? 如果存在, 请求出所有符合条件的点
相似? 如果存在, 请求出所有符合条件的点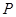 的坐标; 如果不存在, 请说明理由.
的坐标; 如果不存在, 请说明理由.
已知: ,求代数式
,求代数式 的值.
的值.
如图,在△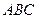 中,
中,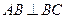 ,
, 于
于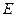 ,点
,点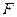 在线段
在线段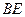 上,
上,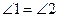 ,点
,点 在线段
在线段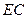 上,请你从以下两个条件中选择一个作为条件,证明△
上,请你从以下两个条件中选择一个作为条件,证明△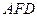 ≌△
≌△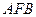 .
.
(1) ∥
∥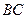 ;
;
(2)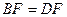 .
.
 .
.
已知:如图,抛物线 与
与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 、
、 两点,点
两点,点 的坐标为
的坐标为 .
.
(1)求抛物线的解析式及顶点 的坐标;
的坐标;
(2)设点 是在第一象限内抛物线上的一个动点,求使与四边形
是在第一象限内抛物线上的一个动点,求使与四边形 面积相等的四边形
面积相等的四边形 的点
的点 的坐标;
的坐标;
(3)求 的面积.
的面积.
已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.
(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7 ,AE=
,AE= ,
,
求tan∠BCP的值.