为了使初三学生在中考中取得好成绩，我区组织了初三中考复习电视讲座，并且就初三学生对中考复习电视讲座了解程度随机抽取了部分学生进行问卷调查，并根据收集的信息进行了统计，绘制了下面尚不完整的统计图．根据统计图中所提供的信息解答下列问题：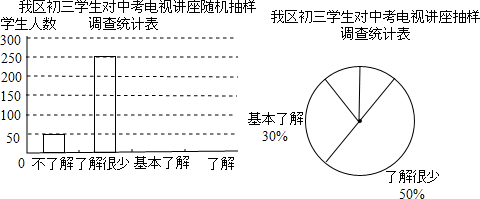
（1）我区参加随机抽取问卷调查的学生有____名；
（2）补全条形统计图；
（3）我区今年初三有近5000名初三学生，请你根据调查的数据计算一下，我区大约有多少名初三学生对中考电视讲座达到基本了解以上（含基本了解）程度？
（4）为了让更多的学生更好的了解该讲座，使中考复习电视讲座发挥其应有的作用，我区举办了两期专栏宣传之后又进行了一次调查，结果发现每期专栏宣传使学生达到基本了解程度以上（含基本了解）的平均增长率是50%，请你求出两期专栏宣传之后学生对此电视讲座达到基本了解以上程度（含基本了解）的人数．
随着“微博潮”的流行，初中学生也开始忙着“织围脖”，某校在上微博的280名学生中随机抽取了部分学生调查他们平常每天上微博的时间，绘制了扇形统计图和频数分布直方图，请根据图中信息，回答下列问题：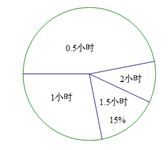
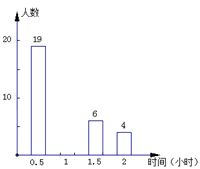
（1）本次共抽取了名学生，将频数分布直方图补充完整；
（2）被调查的学生中上微博的时间中位数落在这一小组内；
（3）样本中，平均每天上微博的时间为0.5小时这一组的频率是；
（4）请估计该校上微博的学生中，大约有名学生平均每天上微博的时间不少于1小时；
某公园有一圆弧形的拱桥，如图已知拱桥所在的圆的半径为10米，拱桥顶
到水面
距离
米．
（1）求水面宽度的大小；
（2）当水面上升到
时，从点
测得桥顶的仰角为
，若
=3，求水面上升的高度．
解方程组：
．
如图，⊙
的半径为6，线段
与⊙相交于点
、
，
，
，
与⊙相交于点
，设
，
．
（1）求
长；
（2）求
关于
的函数解析式，并写出定义域；
（3）当
⊥
时，求
的长．
如图，直线
与
轴、
轴分别相交于点
、
．抛物线
与轴的正半轴相交于点
，与这个一次函数的图像相交于、
，且
．
（1）求点、、的坐标；
（2）如果
，求抛物线
的解析式．