如图，以OA1＝2为底边做等腰三角形，使得第三个顶点C1恰好在直线y=x+2上，并以此向左、右依次类推，作一系列底边为2，第三个顶点在直线y=x+2上的等腰三角形．
（1）请你通过计算说明：底边为2，顶点在直线y=x+2上且面积为21的等腰三角形位于图
中什么位置？
（2）求证：y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半（如：S右1=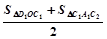
，S右2=
）．
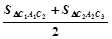（3）过D1、A1、C2三点画抛物线．问在抛物线上是否存在点P，使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的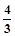
．若存在，请求出点P的坐标；若不存在，请说明理由．
如图，已知CD⊥AB于D，BE⊥AC于E，CD交BE于点O．
若OC=OB，求证：点O在∠BAC的平分线上
若点O在∠BAC的平分线上，求证：OC=OB
已知，如图A、F、C、D四点在一直线上，AF=CD，AB//DE，且AB=DE，求证：
△ABC≌△DEF
∠CBF=∠FEC
如图，AD是∠BAC的平分线，DE⊥AB于点E，DF⊥AC于点F，且DB=DC。求证：BE=CF
如图，（1）画出△ABC关于y轴的对称图形△A1B1C1；
直接写出△ABC关于x轴对称的三角形△A2B2C2的各点坐标。
如图在△ABC 中，AC=BC，
ACB=
，CD
AB，垂足为D，点E在AC上，
CE=EA， BE交CD于点G，EFBE交AB于点F，探索线段EF与EG的数量关系，
并证明你的结论。