已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
如图,已知△ABC中,AB=AC,AB的垂直平分线交AB于D,交AC于E,若△ABC与△EBC的周长分别是26cm、18cm,求AC的值。
如图,△ABC中,BD平分∠ABC,过D作DE∥AB交BC于E,DF∥BC交AB于F。求证:四边形BFDE为菱形。
已知如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE
求证:(1)△AFD≌△CEB
(2)四边形ABCD是平行四边形
如图,Rt△ABC中,∠C="90°," ∠A="60°,AC=2." 按以下步骤作图: ①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D; ②分别以D、E为圆心,以大于 DE长为半径画弧,两弧相交于点P; ③连结AP交BC于点F.那么:
DE长为半径画弧,两弧相交于点P; ③连结AP交BC于点F.那么: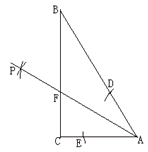
(1)AB的长等于__________;(直接填写答案)
(2)∠CAF ="_________°." (直接填写答案)