如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=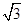 ,BD=CD=1,另一个侧面是正三角形
,BD=CD=1,另一个侧面是正三角形
(1)求证:AD^BC
(2)求二面角B-AC-D的大小
(3)在直线AC上是否存在一点E,使ED与面BCD成30°角?若存在,确定E的位置;若
不存在,说明理由.
(本题10分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入的资金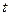 (万元)的关系满足公式P=
(万元)的关系满足公式P=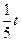 ,Q=
,Q=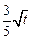 ,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
,现将3万元资金投入经营甲、乙两种商品,设投入乙的资金为x万元,获得的总利润为y(万元)
(1)用x表示y,并指出函数的定义城
(2)当x为何值时,y有最大值,并求出这个最大值
(本题10分)已知函数 是奇函数,且
是奇函数,且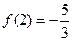 .
.
(1)求函数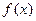 的解析式;
的解析式;
(2)求函数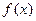 在区间
在区间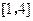 上的最小值.
上的最小值.
(本题10分)设函数 的定义域为A,
的定义域为A,  的定义域为B.(1)求A;(2)若
的定义域为B.(1)求A;(2)若 ,求实数a的取值范围
,求实数a的取值范围
(本小题分14分)已知函数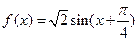
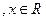
(Ⅰ)求 的最小正周期T;
的最小正周期T;
(Ⅱ)求 的最大值和最小值;
的最大值和最小值;
(Ⅲ)求当 取最大值时
取最大值时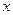 值的集合。
值的集合。
(本小题满分14分)已知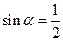 , (1)求角
, (1)求角 所在象限;(2)求
所在象限;(2)求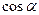 及
及 的值。
的值。