如图所示，竖直光滑直轨道OA高度为2R，连接半径为R的半圆形光滑环形管道ABC（B为最低点），其后连接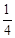
圆弧环形粗糙管道CD，半径也为R．一个质量为m的小球从O点由静止释放，自由下落至A点进入环形轨道，从D点水平飞出，下落高度刚好为R时，垂直落在倾角为30°的斜面上P点，不计空气阻力，重力加速度为g．求：
（1）小球运动到B点时对轨道的压力大小；
（2）小球运动到D点时的速度大小；
（3）小球在环形轨道中运动时，摩擦力对小球做了多少功？
如图所示，面积为0.2 m2的100匝线圈处在匀强磁场中，磁场方向垂直于线圈平面.已知磁感应强度随时
间变化的规律如图，定值电阻R1="6" Ω，线圈电阻R2="4" Ω，求：
（1）在图中标出流过R1的电流方向
(2) 回路中的感应电动势
大小；
如图所示，在倾角
的足够长的固定的斜面底端有一质量m＝1.0kg的物体．物体与斜面间动摩擦因数µ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动．拉力F＝10N，方向平行斜面向上．经时间t＝4s绳子突然断了，(sin37°＝0.60 cos37°＝0.80，g＝10m/s2）
求：（1）绳断时物体的速度大小．
（2）从开始运动到物体上升到斜面最高点的过程中，在斜面上运动的距离．
(3) 物体再回到斜面底端时的速度大小.
A、B两列火车在同一平直轨道上同向匀速行驶，A在前，速度为
=10m/s，B车在后，速度
=30m/s，因大雾能见度低，B车在距A车500m时，才
发现前方有A车．这时B车立即刹车，但要经过1800m B车才能停止.求：
（1）B车刹车过程中的加速度？
（2）A车若仍按原速前进，通过计算分析两车是否会相撞？
如图所示，质量为M=50kg的
人通过跨过定滑轮的轻绳牵引质量为m=20kg的物体，当绳与水平面成60o角时，物体静止不动，不计滑轮与绳的摩擦，g=10
求: 地面对人的摩擦
力和人对地面的压力
从离地面500m的空中自由落下一个小球，不计空气阻力，取g=10
，问：
（1）小球落地前瞬间的速度是多大？
（2）小球到达地面前最后
1s内下落的位移有多大？