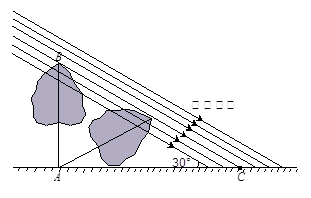
某工厂生产一种产品,当生产数量至少为10吨,但不超过50吨时,每吨的成本y(万元/吨)与生产数量x(吨)的函数关系式如图所示.
(1)求y关于x的函数解析式,并写出它的定义域;
(2)当生产这种产品的总成本为280万元时,求该产品的生产数量.
(注:总成本=每吨的成本×生产数量)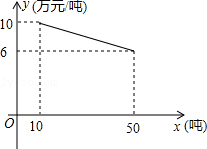
小明家准备建造长为28米的蔬菜大棚,示意图如图(1).它的横截面为如图(2)所示的四边形 ,已知
,已知 米,
米, 米,
米, ,
, ,
, 到
到 的距离
的距离 为1米.矩形棚顶
为1米.矩形棚顶 及矩形
及矩形 由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
由钢架及塑料薄膜制作,造价为每平方米120元,其它部分(保温墙体等)造价共9250元,则这个大棚的总造价为多少元?(精确到1元)
(下列数据可供参考 )
)
根据潍坊市2006年第一季度劳动力市场职业供求状况分析,其中10个职业(职业小类)的需求人数(百人)和求职人数(百人)的数据表格如下:
| 职业 |
纺织工 |
车工 |
电子元器件制造工 |
电焊工 |
保险业务人员 |
行政办公人员 |
财会人员 |
文秘、打字员 |
卫生职业技术人员 |
计算机操作员 |
| 需求人数(百人) |
163 |
123 |
87 |
51 |
33 |
12 |
19 |
11 |
4 |
5 |
| 求职人数(百人) |
71 |
53 |
29 |
22 |
20 |
49 |
52 |
37 |
15 |
14 |
(1)写出求职人数(百人)的中位数;
(2)仿照图中需求人数折线图,画出求职人数的折线图;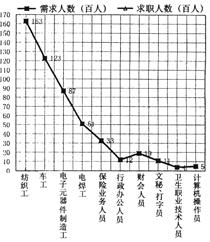
(3)观察图表,比较需求人数与求职人数,你得到什么结论.(只需写出2至3项即可)
已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为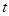 (秒).
(秒). 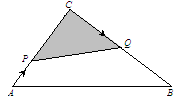
(1)当时间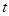 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间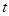 的函数关系式,并指出自变量
的函数关系式,并指出自变量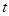 的取值范围;
的取值范围;
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由.
在“五一黄金周”期间,小明和他的父母坐游船从甲地到乙地观光,在售票大厅看到表(一), 爸爸对小明说:“我来考考你,你能知道里程与票价之间有何关系吗?”小明点了点头说:“里程与票价是一次函数关系,具体是……”.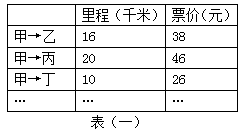
在游船上,他注意到表(二),思考一下,对爸爸说:“若游船在静水中的速度不变,那么我还能算出它的速度和水流速度.”爸爸说:“你真聪明!”亲爱的同学,你知道小明是如何求出的吗?请你和小明一起求出: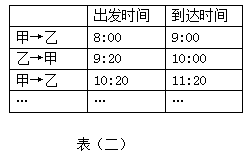
(1)票价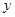 (元)与里程
(元)与里程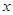 (千米)的函数关系式;
(千米)的函数关系式;
(2)游船在静水中的速度和水流速度.
某数学兴趣小组,利用树影测量树高.已测出树AB的影长AC为9米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变,试求树影的最大长度.
(计算结果精确到0.1米,参考数据: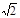 ≈1.414,
≈1.414, 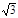 ≈1.732)
≈1.732)