已知椭圆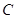
的中心在原点，一个焦点
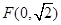，且长轴长与短轴长的比是
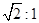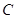．若椭圆在第一象限的一点
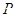的横坐标为1，过点
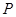作倾斜角互补的两条不同的直线
，
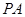分别交椭圆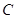于另外两点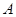
，
.
（Ⅰ）求椭圆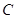的方程；
（Ⅱ）求证：直线
的斜率为定值；
（Ⅲ）求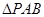
面积的最大值．
设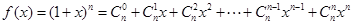
（
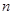是正整数），利用赋值法解决下列问题：
（1）求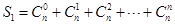
；
（2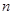）为偶数时，求
；
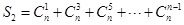（3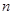）是3的倍数时，求
。
已知：对于任意的多项式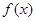
与任意复数z，
整除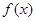。利用上述定理解决下列问题：
在复数范围内分解因式：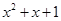
；
求所有满足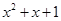整除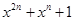
的正整数n构成的集合A。
如图,已知正三棱柱ABC－A1B1C1的底面边长为8，侧棱长为6，D为AC中点。
（1）求证：直线AB1∥平面C1DB；
（2）求异面直线AB1与BC1所成角的余弦值
如图，AB是底面半径为1的圆柱的一条母线，O为下底面中心，BC是下底面的一条切线。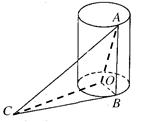
（1）求证：OB⊥AC；
（2）若AC与圆柱下底面所成的角为30°，OA=2。求三棱锥A-BOC的体积。
设函数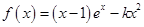
(其中
).
（1）当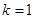
时,求函数
的单调区间;
（2）当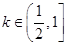
时,求函数在
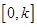上的最大值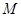
.