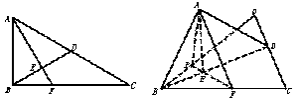甲乙两人进行象棋比赛，规定：每次胜者得1分，负者得0分；当其中一人的得分比另一人的得分多2分时则赢得这场比赛，此时比赛结束；同时规定比赛的次数最多不超过6次，即经6次比赛，得分多者赢得比赛，得分相等为和局。已知每次比赛甲获胜的概率为
，乙获胜的概率为
，假定各次比赛相互独立，比赛经ξ次结束，求：
（1）ξ=2的概率；
（2）随机变量ξ的分布列及数学期望。
件，每个元件的库存费为每年2元，如果不计其他费用，请你帮公司计算，每年进货几次花费最小？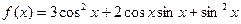
．
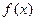的单调递增区间．
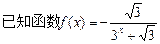
(1)求证：函数y=f(x)的图象关于点（0.5，－0.5）对称；
(2)求f(-2)+f(-1)+f(0)+f(1)+f(2)+f(3)的值;
已知动圆过定点P（1，0），且与定直线L:x=-1相切，点C在l上.
(1)求动圆圆心的轨迹M的方程；
（i）问：△ABC能否为正三角形？若能，求点C的坐标；若不能，说明理由
（ii）当△ABC为钝角三角形时，求这种点C的纵坐标的取值范围.
在Rt△ABC中，∠ACB=30°，∠B=90°，D为AC中点，E为BD的中点，AE的延长线交BC于F，将△ABD沿BD折起，二面角A-BD-C大小记为θ.
（Ⅰ）求证：面AEF⊥面BCD；
（Ⅱ）θ为何值时，AB⊥CD.