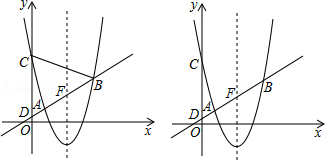
如图,二次函数 的图像交
的图像交 轴于
轴于 ,交
,交 轴于
轴于 ,过
,过 画直线。
画直线。
(1)求二次函数的解析式;
(2)点 在
在 轴正半轴上,且
轴正半轴上,且 ,求
,求 的长;
的长;
(3)点 在二次函数图像上,以
在二次函数图像上,以 为圆心的圆与直线
为圆心的圆与直线 相切,切点为
相切,切点为 。
。
① 点 在
在 轴右侧,且
轴右侧,且 (点
(点 与点
与点 对应),求点
对应),求点 的坐标;
的坐标;
② 若 的半径为
的半径为 ,求点
,求点 的坐标。
的坐标。
已知:如图,以等边 的边 为直径作 ,分别交 , 于点 , ,过点 作 交 于点 .
(1)求证: 是 的切线;
(2)若等边 的边长为8,求由 、 、 围成的阴影部分面积.

“绿水青山就是金山银山”的理念已融入人们的日常生活中,因此,越来越多的人喜欢骑自行车出行.某自行车店在销售某型号自行车时,以高出进价的 标价.已知按标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同.
(1)求该型号自行车的进价和标价分别是多少元?
(2)若该型号自行车的进价不变,按(1)中的标价出售,该店平均每月可售出51辆;若每辆自行车每降价20元,每月可多售出3辆,求该型号自行车降价多少元时,每月获利最大?最大利润是多少?
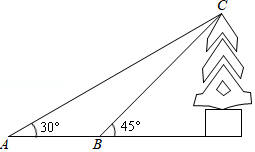
在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度.用测角仪在 处测得雕塑顶端点 的仰角为 ,再往雕塑方向前进4米至 处,测得仰角为 .问:该雕塑有多高?(测角仪高度忽略不计,结果不取近似值.
为调查达州市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :电动车, :公交车, :家庭汽车, :其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
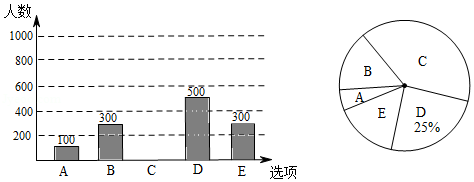
(1)本次调查中,一共调查了 2000 名市民;扇形统计图中, 项对应的扇形圆心角是 度;补全条形统计图;
(2)若甲、乙两人上班时从 、 、 、 四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
如图,在平面直角坐标系 中,以直线 对称轴的抛物线 与直线 交于 , 两点,与 轴交于 ,直线 与 轴交于点 .
(1)求抛物线的函数表达式;
(2)设直线 与抛物线的对称轴的交点为 , 是抛物线上位于对称轴右侧的一点,若 ,且 与 面积相等,求点 的坐标;
(3)若在 轴上有且仅有一点 ,使 ,求 的值.