阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如: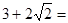
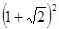 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设
 (其中
(其中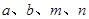 均为整数),则有
均为整数),则有
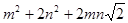 . ∴
. ∴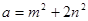 ,
, .
.
这样小明就找到了一种把部分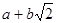 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当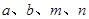 均为正整数时,若
均为正整数时,若
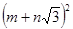 ,用含
,用含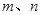 的式子分别表示
的式子分别表示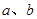 ,得
,得 =_ ,
=_ ,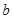 =_ ;
=_ ;
(2)利用上面结论,找一组正整数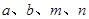 ,填空_ +_ =(_ +_ )
,填空_ +_ =(_ +_ ) ;
;
(3)若
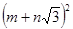 ,且
,且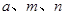 均为正整数,求a的值.
均为正整数,求a的值.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥OC,
OC与BD交于E,若AO=2,BC=2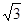 ,求:
,求:
(1)求∠A的度数;(2)求DE的长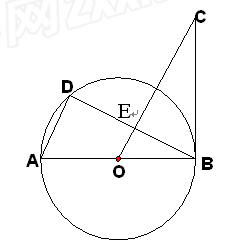
如图,一部起重机的机身AD高22m,吊杆AB长40m,吊杆与水平线的夹角∠BAC可从30°升到80°.分别求起重机起吊过程中的最大水平距离和起重机起吊的离地面最大高度(吊钩本身的长度和所挂重物的高度忽略不计)。
(结果精确到0.1米,sin80°=0.9848,cos80°=0.1736, 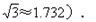

在如图的方格纸中,每个小方格都是边长为1个单位的正方形,
的三个顶点 都在格点上(每个小方格的顶点叫格点).
(1)画出 关于点
关于点 的中心对称的
的中心对称的 ;如果建立直角坐标系,使点B的坐标为
;如果建立直角坐标系,使点B的坐标为
(-5,2),点C的坐标为(-2,2),则点A1的坐标为▲;
(2) 画出 绕点
绕点 顺时针旋转
顺时针旋转 后的
后的 ,并求线段BC扫过的面积.
,并求线段BC扫过的面积.
如图,已知:梯形ABCD中,AD∥BC,E为对角线AC的中点,连结
DE并延长交BC于点F,连结AF.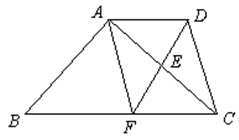
(1)求证:AD=CF;
(2)在原有条件不变的情况下,当AC满足条件▲时(不再增添辅助线),四边形AFCD成为菱形,
(1)计算: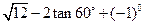 .
.
(2)解方程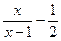 =0
=0