如图，在平面直角坐标系中，矩形OABC的顶点A(0，3)、C(－1，0)．将矩形OABC绕原点O顺时针方向旋转90o，得到矩形OA′B′C′．设直线BB′与x轴交于点M、与y轴交于点N，抛物线经过点C、M、N．解答下列问题：
(1)求直线BB′的 函数解析式；
(2)求抛物线的解析式；
(3)在抛物线上求出使S△PB′′ C′=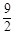
S矩形OABC的所有点P的坐标． 
如图是若干张卡片，它们的背面都一样，现将它们背面朝上，从中任意摸一张卡片，摸到几号卡片的可能性大？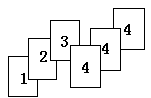
一个均匀的小正方体的各个面上标有1，2，3，4，5，6，将这个小正方体连掷4次，将每次朝上的数字填入四个方框中的任意一个，求所得到的最大四位数和最小四位数各是什么？你认为得到这两种数的可能性哪个大？
某同学发明了一个游戏:掷两个各面上标有1,2,3,4,5,6的均匀的骰子, 用两次朝上的点数相乘,得到一个乘积,如果积为奇数,A胜,结果得到偶数,B胜,你认为这个游戏公平吗?试一试,检验它是否公平.
一张卡片上写着5个数,-3,-6,2,5,6,如图中是一个可以自由转动的转盘.
(1)求出卡片上5个数的平均数.
(2)转动转盘,当转舟停止转动时,根据指针落在的区域所写的内容,改动卡片上的数据,或增加、减少卡片上数的个数,以满足要求.
(3)多做几次,这时卡片上数字的平均数增大了还是减小了? 说说你对这个游戏的认识.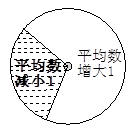
用10个球设计一个摸球游戏，使摸到红球的可能性比摸到蓝球的可能性大。