如图,经过原点的抛物线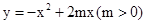 与
与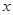 轴的另一个交点为A.过点
轴的另一个交点为A.过点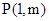 作直线
作直线 轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连结CB,CP。
(1)当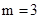 时,求点A的坐标及BC的长;
时,求点A的坐标及BC的长;
(2)当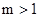 时,连结CA,问
时,连结CA,问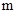 为何值时CA⊥CP?
为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在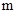 ,使得点E落在坐标轴上?若存在,求出所有满足要求的
,使得点E落在坐标轴上?若存在,求出所有满足要求的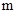 的值,并写出相对应的点E坐标;若不存在,请说明理由。
的值,并写出相对应的点E坐标;若不存在,请说明理由。
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
(1)若设图中最大正方形B的边长是x米,请用含x的代数式表示出正方形F、E和C的边长分别为 , , ;
(2)观察图形可知,长方形相对的两边是相等的(如图中的MN和PQ),请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙两个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
某市规定如下用水收费标准:每户每月用水不超过6立方米时,水费按每立方米a元收费;超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按b元收费.该市某户今年3、4月份的用水量和水费如下表所示:
| 月份 |
用水量(立方米) |
水费(元) |
| 3 |
5 |
7.5 |
| 4 |
9 |
27 |
(1)求出a与b的值;
(2)求当用户用水为x立方米时的水费(用含x的代数式表示);
(3)某用户某月交水费39元,这个月该用户用水多少立方米?
请按下列要求作图.
①将图1中阴影图形围绕点O,按顺时针方向旋转180°;
②将图2中阴影图形向右平移2个单位,在向下平移3个单位;
③将图3中阴影图形沿着OA所在直线翻折。
如图,已知线段AB=6,延长线段AB到C,使BC=2AB,点D是AC的中点.
求:(1)AC的长;
(2)BD的长.
已知关于x的方程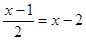 与方程
与方程 的解相等,求m的值.
的解相等,求m的值.