如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数 (k≠0)在第一象限内的图象经过点D、E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D、E,且tan∠BOA= .
.
(1)求边AB的长;
(2)求反比例函数的解析式和n的值;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.
如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,AE=CE,AB与CF有什么位置关系?说明你作出判断的理由.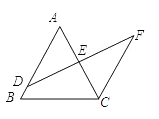
如图,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个?(并用直尺与圆规画出相应的等腰三角形)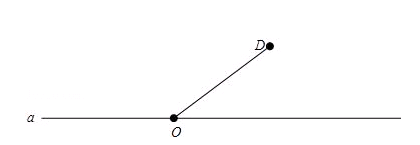
如图,∠1=100°,∠2=100°,∠3=120°,填空: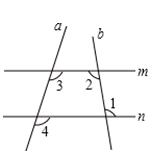
∵∠1=∠2=100°(已知)
∴ _______ ∥ _______ (内错角相等,两直线平行)
∴∠ ______ =∠ _____ (两直线平行,同位角相等)
又∵∠3=120°(已知)
∴∠4= _____ 度.
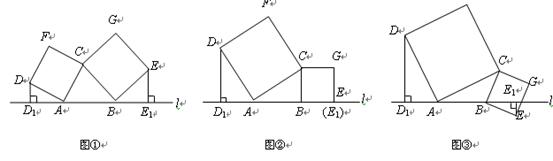
如图①所示,已知 、
、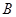 为直线
为直线 上两点,点
上两点,点 为直线
为直线 上方一动点,连接
上方一动点,连接 、
、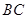 ,分别以
,分别以 、
、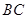 为边向
为边向 外作正方形
外作正方形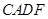 和正方形
和正方形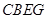 ,过点
,过点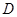 作
作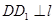 于点
于点 ,过点
,过点 作
作 于点
于点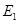 .
.
(1)如图②,当点 恰好在直线
恰好在直线 上时(此时
上时(此时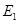 与
与 重合),试说明
重合),试说明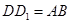 ;
;
(2)在图①中,当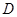 、
、 两点都在直线
两点都在直线 的上方时,试探求三条线段
的上方时,试探求三条线段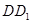 、
、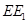 、
、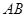 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)如图③,当点 在直线
在直线 的下方时,请直接写出三条线段
的下方时,请直接写出三条线段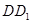 、
、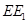 、
、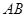 之间的数量关系.(不需要证明)
之间的数量关系.(不需要证明)
(1) 如图1,在正方形ABCD中,点E,F分别在边BC,CD上,AE,BF交于点O,∠AOF=90°.求证:BE=CF.
(2) 如图2,在正方形ABCD中,点E,H,F,G分别在边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°, EF=4.求GH的长.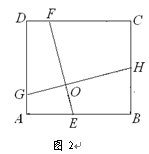
(3) 已知点E,H,F,G分别在矩形ABCD的边AB,BC,CD,DA上,EF,GH交于点O,∠FOH=90°,EF=4. 直接写出下列两题的答案:
①如图3,矩形ABCD由2个全等的正方形组成,求GH的长;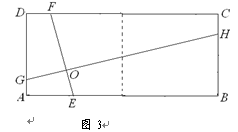
②如图4,矩形ABCD由n个全等的正方形组成,求GH的长(用n的代数式表示).