某中学九年级甲、乙两班同学商定举行一次远足活动,A、B两地相离10千米,甲班从A地出发匀速步行到B地,乙班从B地出发匀速步行到A地,两班同学各自到达目的地后都就地活动. 两班同时出发,相向而行. 设步行时间为x小时,甲、乙两班离A地的距离分别为y1千米、y2千米,y1、y2与x的函数关系图象如图所示,根据图象解答下列问题:
分别求出y1、y2与x的函数关系式
求甲、乙两班学生出发后,几小时相遇?
下面图①,图②是某校随机调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图:
根据上图信息,解答下列问题求本次被调查学生的人数,并补全条形统计图
若全校共有1620名学生,你估计这所学校有多少名学生知道母亲的生日?
通过对以上数据的分析,你有何感想?(用一句话回答)
如图是某区“平改坡”工程中一种坡屋顶的设计图.已知原平屋顶的宽度AB为8米, 两条相等的斜面钢条AC、BC夹角为110°,过点C作CD⊥AB于D.求坡屋顶高度CD的长度;
求斜面钢条AC的长度.(长度精确到0.1米)

先化简,再求值: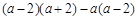 ,其中
,其中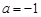 .
.
计算: .
.