从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下: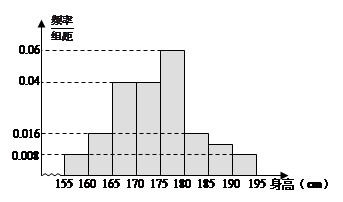
(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
已知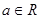 ,设函数
,设函数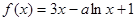
(1)若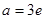
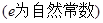 ,求函数
,求函数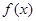 在
在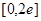 上的最小值
上的最小值
(2)判断函数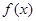 的单调性
的单调性
在极坐标系下,设圆C: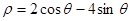 ,试求:
,试求:
(1)圆心的直角坐标表示
(2)在直角坐标系中,设曲线C经过变换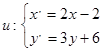 得到曲线
得到曲线 ,则曲线
,则曲线 的轨迹是什么图形?
的轨迹是什么图形?
已知函数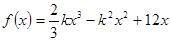 ,是否存在实数
,是否存在实数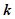 ,使函数在
,使函数在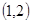 上递减,在
上递减,在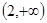 上递增?若存在,求出所有
上递增?若存在,求出所有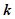 值;若不存在,请说明理由.
值;若不存在,请说明理由.
已知 ,复数
,复数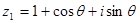 ,
,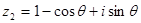 .
.
(1)当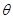 取何值时,
取何值时,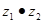 是实数;
是实数;
(2)求证: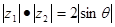 .
.
甲、乙两个班级进行一次数学考试,按照成绩分为优秀和不优秀两种情况,统计成绩后发现,甲班45名学生中有35人考试成绩不优秀 ,乙班45名学生中有7人考试成绩优秀,试分析:
(1)估计甲班学生数学考试成绩的优秀率
(2)能否有99%的把握认为数学考试成绩优秀与 班级有关?
附: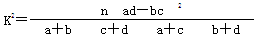 (其中
(其中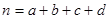 )
)
临界值表
| P(K2≥k) |
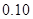 |
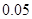 |
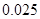 |
 |
 |
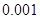 |
| k |
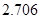 |
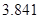 |
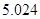 |
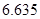 |
 |
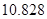 |