甲、乙两个班级进行一次数学考试,按照成绩分为优秀和不优秀两种情况,统计成绩后发现,甲班45名学生中有35人考试成绩不优秀 ,乙班45名学生中有7人考试成绩优秀,试分析:
(1)估计甲班学生数学考试成绩的优秀率
(2)能否有99%的把握认为数学考试成绩优秀与 班级有关?
附: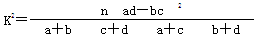 (其中
(其中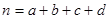 )
)
临界值表
| P(K2≥k) |
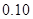 |
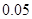 |
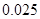 |
 |
 |
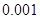 |
| k |
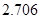 |
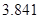 |
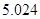 |
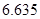 |
 |
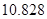 |
设函数 =
= 的图象的对称中心为点(1,1).
的图象的对称中心为点(1,1).
(1)求 的值;
的值;
(2)若直线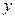 =
=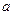 (
(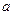 ∈R)与
∈R)与 的图象无公共点,且
的图象无公共点,且 <2
<2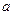 +
+ ,求实数
,求实数 的取值范围.
的取值范围.
己知函数 的定义域为
的定义域为 , 函数
, 函数 的值域为
的值域为 ,不等式
,不等式 的解集为
的解集为
(1)求A
(2)若同时满足A,B的 值也满足C,求
值也满足C,求 的取值范围;
的取值范围;
(  13分)设函数
13分)设函数
(1)研究函数
 的单调性;
的单调性;
(2)判断 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.
已知圆
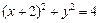 ,相互垂直的两条直线
,相互垂直的两条直线 、
、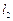 都过点
都过点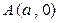 .
.
(Ⅰ)当 时,若圆心为
时,若圆心为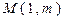 的圆和圆
的圆和圆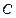 外切且与直线
外切且与直线 、
、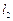 都相切,求圆
都相切,求圆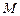 的方程;
的方程;
(Ⅱ)当 时,求
时,求 、
、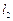 被圆
被圆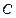 所截得
所截得 弦长之和的最大值.
弦长之和的最大值.
如图,当甲船位于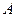 处时获悉,在其正东方向相距20海里的
处时获悉,在其正东方向相距20海里的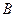 处有一艘渔船遇险
处有一艘渔船遇险 等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30
等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30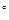 ,相距10海里
,相距10海里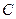 处的乙船.
处的乙船.
(Ⅰ)求处于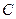 处的乙船和遇险渔船间的距离;
处的乙船和遇险渔船间的距离;
(Ⅱ)设乙船沿直线 方向前往
方向前往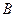 处救援,其方向与
处救援,其方向与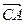 成
成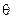 角,求
角,求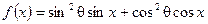
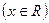 的值域.
的值域.