已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (
( 为坐标原点),求实数
为坐标原点),求实数 取值范围.
取值范围.
已知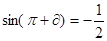 ,计算:
,计算:
(1) ;(2)
;(2) ;(3)
;(3) ;(4)
;(4)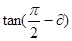 ;
;
已知tanα=- .
.
(1)求α的其它三角函数的值;
(2)求 的值.
的值.
两枚质量均匀的正方体骰子,六个面上分别标有数字1、2、3、4、5、6,抛掷两枚骰子.记两枚骰子朝上的面上的数字分别为p,q,若把p,q分别作为点A的横坐标和纵坐标,
(1)用列表法或树状图表示出点A(p,q)所有可能出现的结果;
(2)求点A(p,q)在函数y=x-1的图象上的概率.
已知圆心为C的圆经过点A(-1,1)和B(-2,-2),且圆心在直线L:x+y-1=0上,求圆心为C的圆的标准方程.
探究函数f(x)=x+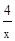 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中y值随x值变化的特点,完成以下的问题.
函数f(x)=x+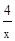 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;
(1)函数f(x)=x+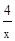 (x>0)在区间上递增.
(x>0)在区间上递增.
当x=时,y最小=.
(2)证明:函数f(x)=x+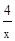 在区间(0,2)上递减.
在区间(0,2)上递减.
(3)思考:函数f(x)=x+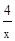 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)