某市为准备参加省中学生运动会，对本市甲、乙两个田径队的所有跳高运动员进行了测试，用茎叶图表示出甲、乙两队运动员本次测试的跳高成绩（单位：cm，且均为整数），同时对全体运动员的成绩绘制了频率分布直方图．跳高成绩在185cm以上（包括185cm）定义为“优秀”，由于某些原因，茎叶图中乙队的部分数据丢失，但已知所有运动员中成绩在190cm以上（包括190cm）的只有两个人，且均在甲队． 
（Ⅰ）求甲、乙两队运动员的总人数a及乙队中成绩在[160,170）（单位：cm）内的运动员人数b；
（Ⅱ）在甲、乙两队全体成绩为“优秀”的运动员的跳高成绩的平均数和方差；
（Ⅲ）在甲、乙两队中所有的成绩为“优秀”的运动员中随机选取2人参加省中学生运动会正式比赛，
求所选取两名运动员均来自甲队的概率．
（本小题满分12分）
如图，在三棱锥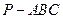
中，
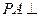底面ABC,
，
AP="AC," 点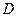
，
分别在棱
上，且BC//平面ADE
（Ⅰ）求
证：DE⊥平面
；
（Ⅱ）当二面角
为直二面角时，求多面体ABCED与PAED的体积比。
（本小题满分12分）
已知函数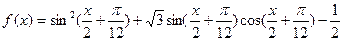
。
（Ⅰ）求
的值域；
（Ⅱ）若（x>0）的图象与直线
交点的横坐标由小到大依次是
，
，…，
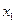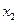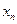，求数列
的前
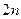项的和。
（本小题满分14分）
已知函数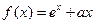
，
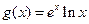.（其中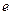
为自然对数的底数），
（Ⅰ）设曲线
在
处的切线与直线
垂直，求
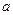的值；
（Ⅱ）若对于任意实数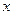
≥0，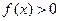
恒成立，试确定实数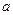的取值范围；
（Ⅲ）当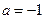
时，是否存在实数
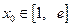，使
曲线C：
在点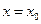
处的切线与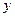
轴垂直？若存在，求出
的值；若不存在，请说明理由.
（本小题满分14分）
已知椭圆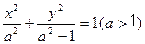
的左右焦点为
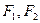，抛物线C：
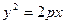以F2为焦点且与椭圆相交于点M
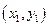、N
，直线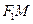
与抛物线C相切
（Ⅰ）求抛物线C的方程和点M、N的坐标；
（Ⅱ）求椭圆的方程和离心率．
（本小题满分14分）
如图，已知三棱锥A—BPC中，AP⊥PC， AC⊥BC，
M为AB中点，D为PB中点，且△PMB为正三角形。
（Ⅰ）求证：DM∥平面APC；
（Ⅱ）求证：平面ABC⊥平面APC；
（Ⅲ）若BC＝4，AB＝20，求三棱锥D—BCM的体积．