有A,B两个黑布袋,A布袋中有两个完全相同的小球,分别标有数字l和2.B布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点Q的一个坐标为(x,y).
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线y=x-3上的概率.
(本题12分)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: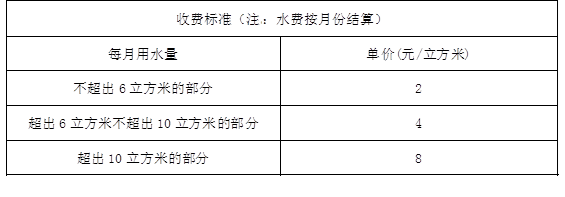
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水 立方米(其中6<
立方米(其中6< <10),请用含
<10),请用含 的代数式表示应收水费.
的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水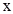 立方米,请用含
立方米,请用含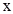 的代数式表示该户居民5、6两个月共交水费多少元?
的代数式表示该户居民5、6两个月共交水费多少元?
(本题10分)如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长.
(本题10分))如图,半径为1个单位的圆片上有一点Q与数轴上的原点重合(提示:圆的周长C=2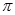 r,
r, 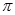 保留).
保留).
(1)把圆片沿数轴滚动1周,点Q到达数轴上点A的位置,点A表示的数是___;
(2)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2, -1, -5, +4, +3, -2.
①第几次滚动后,Q点距离原点最近?第几次滚动后,Q点距离原点最远?
②当圆片结束运动时,Q点运动的路程共有多少?此时点Q所表示的数是多少?
(本题8分)已知已知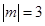 ,
,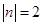 ,且
,且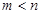 ,求
,求 的值.
的值.
(本题8分)
(1) 求出下列各数:① 2的平方根; ②-27的立方根; ③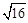 的算术平方根.
的算术平方根.
(2) 将(1)中求出的每个数准确地表示在数轴上.
(3) 将(1)中求出的每个数按从小到大的顺序排列,并用“﹤”连接.