探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图,∠FDC与∠ECD分别为△ADC的两个外角,
试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: _______________________________.
在平面直角坐标系xOy中,二次函数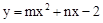 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?
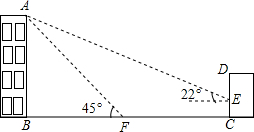
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.(参考数据:sin22º≈ ,cos22º≈
,cos22º≈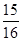 ,tan22º≈
,tan22º≈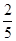 )
)
如图所示,在梯形ABCD中,AD∥BC,∠BDC=90°,E为DC上一点,∠BDE=∠DBC.
(1)求证:DE=CE;
(2)若 ,试判断四边形ABED的形状,并说明理由.
,试判断四边形ABED的形状,并说明理由.
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).

(1)求a和乙的方差S乙;
(2)请你从平均数和方差的角度分析,谁将被选中.