分解因式:(a-b)m2+(b-a)n2;
已知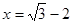 ,求
,求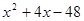 的值.
的值.
已知:点A(2,-2)和点B(1,-4)在一次函数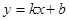 的图象上,
的图象上,
(1)求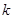 和
和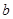 的值;
的值;
(2)求当x=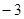 时的函数值.
时的函数值.
如图,抛物线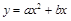 (a
(a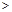 0)与双曲线
0)与双曲线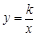 相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
相交于点A,B. 已知点A的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).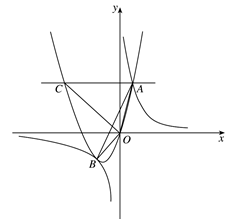
(1)求实数a,b,k的值;
(2)过抛物线上点A作直线AC∥x轴,交抛物线于另一点C,求所有满足△EOC∽△AOB的点E的坐标.(其中点E和点A,点C和点B分别是对应点)
在边长为10的正方形ABCD中,以AB为直径作半圆O,如图①,E是半圆上一动点,过点E作EF⊥AB,垂足为F,连结DE.
(1)当DE=10时,求证:DE与圆O相切;
(2)求DE的最长距离和最短距离;
(3)如图②,建立平面直角坐标系,当DE =10时,试求直线DE的解析式.
在直角坐标系中,点A的坐标是(3,0),点P在第一象限内的直线y=-x+4上.设点P的坐标为(x,y),得到△POA.
(1)在所给直角坐标系中画出符合已知条件的图形;
(2)求△POA的面积S与自变量x的函数关系式及x的取值范围;
(3)若以P、O、A、Q为顶点构成平行四边形,请直接写出第四个顶点Q的坐标.