某中学在一次“爱护环境，节约能源”的活动中，开展了“垃圾分类知多少”专题调查，以随机抽样的方式进行了问卷调查，问卷调查的结果分为A“非常了解”、B“比较了解”、C“基本了解”、D“不太了解”四个阶段，并根据统计数据绘制了图①和图②两幅尚不完整的统计图．
(1)这次随机进行的问卷调查中的样本容量是_______．
(2)调查结果为“基本了解”的频数在扇形图中所对应的扇形圆心角度数是_____，并将图①和图②的统计
图补充完整．
(3)在“比较了解”的调查结果里，初一年级学生共有4人，其中2男2女，在这4人中，打算随机选出2
位进行采访，则所选两位同学中至少有一位是男同学的概率是_______．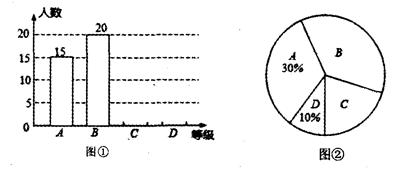
（本题10分）如图，在Rt△ABC中，∠C＝90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB分别交于点D、E，且∠CBD＝∠A．
试判断直线BD与⊙O的位置关系，并证明你的结论．
(10分)小红和小慧玩纸牌游戏．如图是同一副扑克中的4张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小慧从剩余的3张牌中也抽出一张． 
（1）请用树形图表示出两人抽牌可能出现的所有结果；
（2）求抽出的两张牌都是偶数的概率．
在如图的方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上（每个小方格的顶点叫格点）．
（1）如果建立直角坐标系，使点B的坐标为（－5，2），点C的坐标为（－2，2），则点A的坐标为；
（2）画出△ABC绕点O顺时针旋转90°后
的△A1B1C1，并求线段BC扫过的面积．
按下面的要求填空，完成本题的解答．
青山村种的水稻2007年平均每公顷产8 000 kg，2009年平均每公顷产9 680 kg，
求该村水稻每公顷产量的年平均增长率.
解：设该村水稻每公顷产量的年平均增长率为
.
（Ⅰ）用含的代数式表示：
① 2008年种的水稻平均每公顷的产量为kg；
② 2009年种的水稻平均每公顷的产量为kg；
（Ⅱ）根据题意，列出相应方程；
（Ⅲ）解这个方程，得；
（Ⅳ）检验：；
（Ⅴ）答：该村水稻每公顷产量的年平均增长率为%.
若方程
与
有相同的解, 求a的值和这个相同的解.