（1）如图1是一个重要公式的几何解释，请你写出这个公式 ；在推得这个公式的过程中，主要运用了（ ）
| A．分类讨论思想 | B．整体思想 | C．数形结合思想 | D．转化思想 |
（2）如图2，Rt△ABC≌Rt△CDE，∠B=∠D=90°，且B，C，D在同一直线上．求证：∠ACE=90°；
（3）伽菲尔德（1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（发表在1876年4月1日的《新英格兰教育日志》上），请你尝试该证明过程．
图1 图2
（本大题10分）解分式方程：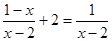
.
（本大题10分）已知不等式：⑴ 1－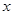
＜0； ⑵
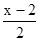＜1；⑶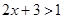
；
⑷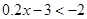 
．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．
开学初，小芳和小亮去学校商店购买学习用品，小芳用18元钱买了1枝钢笔和3本笔记本；小亮用31元买了同样的钢笔2枝和笔记本5本。
（1）求每枝钢笔和每本笔记本的价格；
（2）校运会后，班主任拿出200元学校奖励基金交给班长，购买上述价格的钢笔和笔记本共48件作为奖品，奖给校运会中表现突出的同学，要求笔记本数不少于钢笔数，共有多少种购买方案？请你一一写出。
小雨想用一块面积为400cm2的正方形纸片，沿着边的方向裁出一块面积为300cm2的长方形，使它的长宽之比为3:2，不知能否裁出来，正在发愁，小明见了说：“别发愁，一定能用一块面积大的纸片裁出一块面积小的纸片。”你同意小明的说法吗？小雨能用这块纸片裁出符合要求的纸片吗？
观察下列一组等式：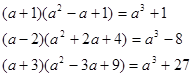
（1）以上这些等式中，你有何发现？利用你的发现填空。
①
②
（）=
③（）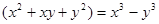
（2）计算：