今年我国许多地方严重的“旱情”，为了鼓励居民节约用水，区政府计划实行两级收费制，即每月用水量不超过14吨（含14吨）时，每吨按政府补贴优惠价收费；每月超过14吨时，超过部分每吨按市场调节价收费．小英家1月份用水20吨，交水费29元；2月份用水18吨，交水费24元．
（1）求每吨水的政府补贴优惠价和市场调节价分别是多少？
（2）设每月用水量为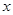
吨，应交水费为y元，写出y与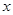之间的函数关系式；
（3）小英家3月份交水费39元，她家应用水多少吨？
为了落实国家的惠农政策，某地政府制定了农户投资购买收割机的补贴办法，其中购买Ⅰ、Ⅱ两型收割机所投资的金额与政府补贴的额度存在下表所示的函数对应关系：
| Ⅰ型收割机 |
Ⅱ型收割机 |
||||
| 投资金额x（万元） |
x |
5 |
x |
2 |
4 |
| 补贴金额y（万元） |
y1=kx |
2 |
y2=ax2+bx |
2.4 |
3.2 |
（1）分别求出y1和y2的函数表达式；
（2）旺叔准备投资10万元购买Ⅰ、Ⅱ两型收割机。请你设计一个能获得最大补贴金额的方案，并求出按此方案能获得的补贴金额。
如图，已知二次函数y=ax2+bx+2的图像经过A（-1，-1），C（1,3）.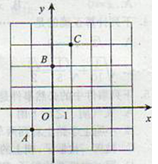
（1）求二次函数的解析式并画出它的图像；
（2）直接写出点A关于抛物线对称轴的对称点A'的坐标；
（3）求该抛物线上到x轴的距离为2的所有点的坐标。
如图所示，二次函数y=-x2+2x+m的图象与x轴的一个交点为A（3,0），另一个交点为B，且与y轴交于点C。
（1）求m的值；
（2）求点B的坐标；
（3）该二次函数图像上有一点D（x,y）（其中x＞0，y＞0），使S△ABD=S△ABC，求点D的坐标。
如图，以线段AB为直径的⊙O交线段AC于点E，点D是AE的中点，连接OD并延长交⊙O于点M，∠BOE=60°，cosC=
，BC=
．
（1）求
的度数；
（2）求证：BC是⊙
的切线；
（3）求弧AM的长度．
如图，反比例函数
（k≠0）的图像过等边三角形AOB的顶点A，已知点B（-2，0）
（1）求反比例函数的表达式；
（2）若要使点B在上述反比例函数的图像上，需将△AOB向上平移多少个单位长度？