(12分)已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
(10分)如图1,O为正方形ABCD的中心,
分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转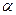 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当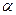 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.
(9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测.某次检测设有A、B两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力.
(1)求甲、乙、丙三名学生在同一处检测视力的概率;
(2)求甲、乙、丙三名学生中至少有两人在B处检测视力的概率.
(8分)比较正五边形与正六边形,可以发现它们的相同点和不同点.例如:
它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.
它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.
请你再写出它们的两个相同点和不同点:
相同点:
① ;
② .
不同点:
① ;
② .
(8分)在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?