已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x="4." 设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图1,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;
(3)如图2,点M是线段OP上的一个动点(O、P两点除外),以每秒 个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN. 在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒. 求S关于t的函数关系式.
个单位长度的速度由点P向点O 运动,过点M作直线MN∥x轴,交PB于点N.将△PMN沿直线MN对折,得到△P1MN. 在动点M的运动过程中,设△P1MN与梯形OMNB的重叠部分的面积为S,运动时间为t秒. 求S关于t的函数关系式. 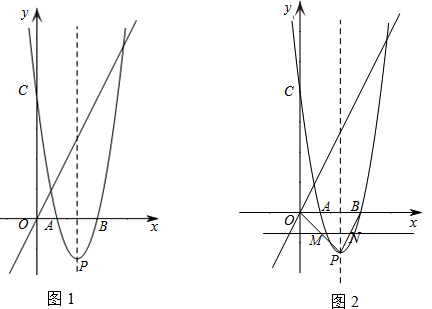
如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= _________ ,PD= _________ .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
如图1所示:等边△ABC中,线段AD为其内角角平分线,过D点的直线B1C1⊥AC于C1交AB的延长线于B1.
(1)请你探究: ,
, 是否都成立?
是否都成立?
(2)请你继续探究:若△ABC为任意三角形,线段AD为其内角角平分线,请问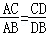 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
(3)如图2所示Rt△ABC中,∠ACB=90︒,AC=8,AB= ,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求
,E为AB上一点且AE=5,CE交其内角角平分线AD于F.试求 的值.
的值.
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm.动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动,以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形和梯形重合部分的面积为Scm2.
(1)当t= _________ s时,点P与点Q重合;
(2)当t= _________ s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,求S与t之间的函数关系式.
如图1,在菱形ABCD中,AC=2,BD=2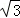 ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.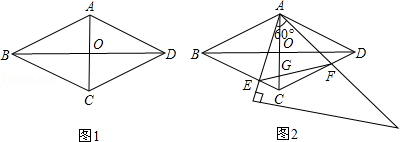
已知:如图,四边形ABCD是正方形,BD是对角线,BE平分∠DBC交DC于E点,交DF于M,F是BC延长线上一点,且CE=CF.
(1)求证:BM⊥DF;
(2)若正方形ABCD的边长为2,求ME•MB.