如图①,△ABC与△DEF为等腰直角三角形,CB与EF重合,AC=DE=8,∠ACB=∠DEF=90°固定△ABC,将△DEF绕点C顺时针旋转,当边FE与边CA重合时,旋转终止。设FE、FD(或它的延长线)分别交AB(或它的延长线)于点P、Q,如图②
(1)问:始终与△CPB相似的三角形(不添加其他辅助线)有① 及②
(2)设BP=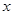 ,AQ=
,AQ=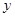 ,求
,求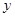 关于
关于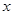 的函数关系式;
的函数关系式;
(3)问:当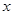 为何值时,△CPQ是等腰三角形?
为何值时,△CPQ是等腰三角形?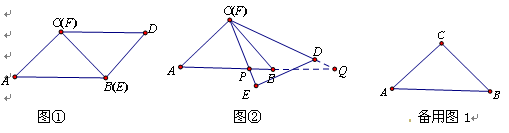
(本题满分12分,其中第(1)小题5分,第(2)小题7分)
已知:如图,斜坡AP的坡度为1∶2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.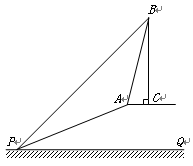
求:(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).
(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
已知:如图,矩形DEFG的一边DE在△ABC的边BC上,顶点G、F分别在边AB、AC上,AH是边BC上的高,AH与GF相交于点K,已知BC=12,AH=6,EF∶GF=1∶2,求矩形DEFG的周长.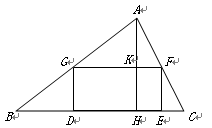
(本题满分10分,其中每小题各5分)
已知:如图,在△ABC中,AB=6,BC=8,∠B=60°
求:(1)△ABC的面积;
(2)∠C的余弦值.
(本题满分10分,其中第(1)小题6分,第(2)小题4分)
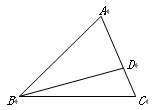
如图,已知在△ABC中,点D在边AC上,CD∶AD=1∶2,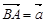 ,
,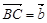 .
.
(1)试用向量
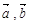 表示向量
表示向量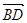 ;
;(2)求作:
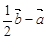 .(不要求写作法,但要指出所作
.(不要求写作法,但要指出所作
图中表示结论的向量)
(本题满分10分,其中第(1)小题4分,第(2)小题6分)
已知抛物线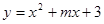 的对称轴为x=-2.
的对称轴为x=-2.(1)求m的值;
(2)如果将此抛物线向右平移5个单位后,求所得抛物线与y轴的交点坐标.