根据图所示的程序，得到了y与x的函数图象，过点M作PQ∥x轴交图象于点P,Q，连接OP,OQ.则以下结论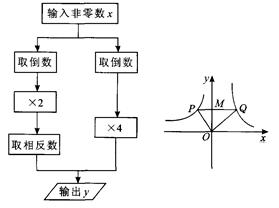
①x＜0时，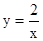
，
②△OPQ的面积为定值，
③x＞0时，y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确的结论是（ ）
| A．①②④ | B．②④⑤ |
| C．③④⑤ | D．②③⑤ |
用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（）
| A．（x+1）2=6 | B．（x﹣1）2=6 | C．（x+2）2=9 | D．（x﹣2）2=9 |
关于x的一元二次方程（a2﹣1）x2+x﹣2=0是一元二次方程，则a满足（）
| A．a≠1 | B．a≠﹣1 | C．a≠±1 | D．为任意实数 |
如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB⇒BC⇒CD⇒DA⇒AB连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向是（）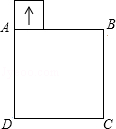
A． |
B． |
C． |
D． |
阅读理解：如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（）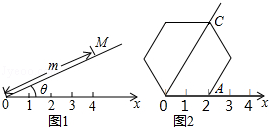
| A．（60°，4） | B．（45°，4） |
C．（60°，2 ） |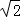
D．（50°，2 ） |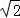
如图，将半径为3的圆形纸片，按下列顺序折叠，若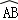
和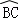
都经过圆心O，则阴影部分的面积是（）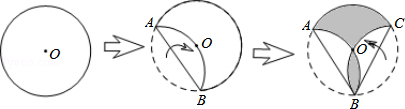
| A．π | B．2π | C．3π | D．4π |