如图,已知 ,
, ,试说明
,试说明 的理由.
的理由.
如图所示, 是
是 的内接三角形,
的内接三角形,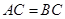 ,
,  为
为 中弧AB上一点,延长
中弧AB上一点,延长 至点
至点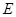 ,使
,使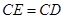 .
.
(1)求证: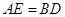 ;
;
(2)若 ,求证:
,求证: .
.
已知A、B、C是半径为2的圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
(1)求证:OD=OE;
(2)连接BC,当BC= 时,求∠DOE的度数.
时,求∠DOE的度数.
如图所示,将正方形ABCD中的△ABD绕对称中心O旋转至△GEF的位置,EF交AB于M,GF交BD于N.请猜想AM与GN有怎样的数量关系?并证明你的结论.
王老师为学校购买某种篮球,体育用品商店老板给出了如下优惠条件:如果一次性购买不超过10个,单价为80元;如果一次性购买多于10个,那么每增加1个,购买的所有篮球的单价降低2元,但单价不得低于50元.按此优惠条件,王老师一次性购买这种篮球付了1200元.请问王老师购买了多少个这种篮球?
已知关于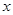 的一元二次方程
的一元二次方程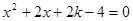 有两个不相等的实数根.
有两个不相等的实数根.
(1)求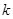 的取值范围;
的取值范围;
(2)若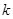 为正整数,且该方程的根都是整数,求
为正整数,且该方程的根都是整数,求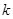 的值.
的值.