已知：抛物线y=x
+bx+c的顶点D在直线y=-4x上，且与x轴的交点A(-1,0),B,交y轴于点C，顶点为D. 
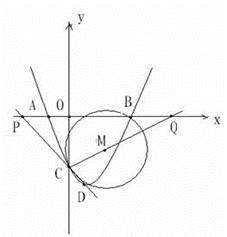
(1) 求抛物线的解析式及顶点D的坐标.
(2)试判断点C与以BD为直径的⊙M的位置关系.
(3)若点P的坐标是（a,0）,是否存在a，使得直线PC是⊙M的切线？若存在，求出a的值,若不存在，请说明理由.
在平面直角坐标系中，点O为原点，抛物线y=ax2+bx（其中-1≤a＜0）经过A（3，n），AB⊥y轴于B，抛物线交直线AB于M．
（1）若n=1，AB=3BM，求抛物线所对应的函数关系式；
（2）若n=a+b，抛物线与x轴另一个异于原点的交点为C，过点A作AP∥OM交直线MC于点P，当△OPM的面积最大时，求sin∠MOP的值．
如图，四边形ABCD是⊙O的内接四边形，
，点E、F分别是弦AD、DC上的点．
（1）若∠ABE=∠CBF，BE=BF．求证：BD是⊙O的直径．
（2）若
，∠D=2∠EBF=90°，AE=ED=2．求DF的长．
已知点A（m，p），B（n，q）（m＜n＜0）在动点C（
，a）（k≠0）所形成的曲线上．若p+q=-b-2，
．试比较p和q的大小，并说明理由．
定义：如果两个一元二次方程有且只有一个相同的实数根，我们称这两个方程为“友好方程”．如果关于x的一元二次方程x2-4x+5m=mx+5与x2+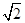
x+m-1=0互为“友好方程”，求m的值．
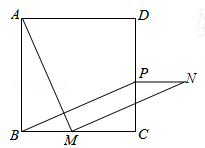
如图，在正方形ABCD中，点M是BC边上的任意一点，连接AM，并将线段AM绕点M顺时针旋转90°得到线段MN，过N作NP⊥C D于点P，连接BP．求证：四边形BMNP是平行四边形