将4个编号为1,2,3,4的不同小球全部放入4个编号为1,2,3,4的4个不同盒子中,求:
(1)每盒至少一个球,有多少种放法?
(2)恰好有一个空盒,有多少种放法?
(3)每盒放一个球,并且恰好有一个球的编号与盒子的编号相同,有多少种放法?
(4)把已知中4个不同的小球换成四个完全相同的小球(无编号),其余条件不变,恰有一个空盒,有多少种放法?
已知 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 在曲线
在曲线 上
上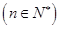 ,且
,且 ,
,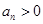 .
.
(1)求数列 的通项公式;
的通项公式;
(2)数列 的前
的前 项和为
项和为 ,且满足
,且满足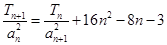 ,
, ,求数列
,求数列 的通项公式;
的通项公式;
(3)求证: ,
, .
.
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度 (单位:
(单位: )满足关系:
)满足关系: (
( ,
, 为常数),若不建隔热层,每年能源消耗费用为
为常数),若不建隔热层,每年能源消耗费用为 万元.设
万元.设 为隔热层建造费用与
为隔热层建造费用与 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求 的值及
的值及 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用 达到最小,并求最小值.
达到最小,并求最小值.
已知单调递增的等比数列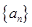 满足:
满足: ,且
,且 是
是 、
、 的等差中项.
的等差中项.
(1)求数列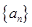 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前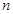 项和
项和 .
.
已知向量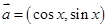 ,
, ,
,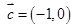
(1)若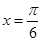 ,求向量
,求向量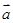 、
、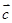 的夹角;
的夹角;
(2)当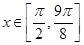 时,求函数
时,求函数 的最大值.
的最大值.
在 中,角
中,角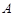 、
、 、
、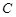 对的边分别为
对的边分别为 、
、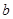 、
、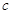 ,且
,且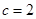 ,
,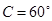 .
.
(1)求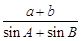 的值;
的值;
(2)若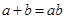 ,求
,求 的面积
的面积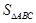 .
.