已知椭圆 的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率 .
.
(1)求椭圆的方程;
(2)设直线 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且 ,求实数m的值.
,求实数m的值.
如图所示的长方体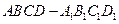 中,底面
中,底面 是边长为
是边长为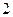 的正方形,
的正方形, 为
为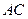 与
与 的交点,
的交点,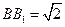 ,
,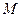 是线段
是线段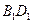 的中点.
的中点.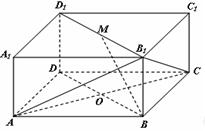
(1)求证: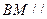 平面
平面 ;
;
(2)求三棱锥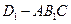 的体积.
的体积.
为研究气候的变化趋势,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度 ,如下表:
,如下表:
(1)若第六、七、八组的频数 、
、 、
、 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出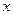 、
、 、
、 、
、 的值;
的值;
(2)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为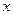 ,
, ,求事件“
,求事件“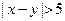 ”的概率.
”的概率.
如图,测量河对岸的塔高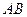 时,可以选与塔底
时,可以选与塔底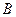 在同一水平面内的两个测点
在同一水平面内的两个测点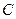 与
与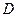 .现
.现 测得
测得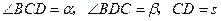 ,并在点
,并在点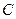 测得塔顶
测得塔顶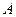 的仰角为
的仰角为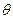 ,求塔高
,求塔高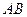 (用题中所给字母表示).
(用题中所给字母表示).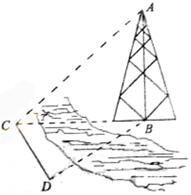
已知函数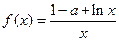 ,
,
(1)求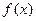 的极值;
的极值;
(2)若关于x的不等式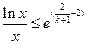 在
在 上恒成立,求k的取值范围;
上恒成立,求k的取值范围;
(3)证明: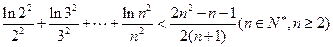 .
.
已知椭圆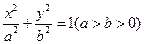 的两焦点
的两焦点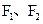 和短轴的两端点
和短轴的两端点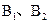 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为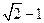 .
.
(1)求椭圆的标准方程;
(2)设P是椭圆上任一点,MN 是圆C: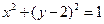 的任一条直径,求
的任一条直径,求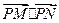 的最大值.
的最大值.